Imaging knowhow

Wavelength of light - Seeing vs. Resolution

The usage of color bandpass filters (red, green, blue) or longpass filters like IR-pass filters or UV-pass filters became quite popular for lunar, solar and planetary imaging lately. Sometimes the filter's impact on resolution is not fully understood. Here's a brief summary of wavelength impacts: Resolution versus Seeing

If a point light source (star) passes a circular aperture (e.g. telescope) a typical diffraction pattern is formed behind the aperture with a bright maximum disc in the center, surrounding concentric rings with decreasing brightness and dark minima in between. The bright central disc is called Airy Disc after George Biddell Airy.


Figure 1: Simulation of diffraction pattern with Airy disc of a perfect scope

The size of the Airy Disc in mm is approximately

x = 2 * 1.22 * lambda * ( f / D )

lambda = wavelength of light in mm
f = focal length in mm
D = aperture diameter in mm

The minimum distance between features a telescope can resolve, easiest case is two point light sources, is related to the size of the Airy disc. There are a few criterions how to calculate the minimum distance between point light sources that a scope can resolve, one is the Rayleigh criterion according to which two point light sources can be told apart at least when the central maximum of one airy disk is located at the first minimum of the other light source:

R[arcsec] = 138 / D[mm] or
R[arcsec] = 5.45 / D[inch]

D = scope aperture

Looking at the formula how to calculate the size of an Airy disc this can be true for a single wavelength only: 550nm (yellow)

Figure 2: Two point light sources separated at Rayleigh limit

D=235mm, f=2350mm

d(lambdaNIR) ~ 2.44 * 700nm * 10 = 0.0171mm
d(lambdaR) ~ 2.44 * 620nm * 10 = 0.0151mm
d(lambdaG) ~ 2.44 * 520nm * 10 = 0.0127mm
d(lambdaB) ~ 2.44 * 450nm * 10 = 0.011mm
d(lambdaNUV) ~ 2.44 * 375nm * 10 = 0.0092mm

Note that the Airy Disc size of near infrared is almost twice the size than of near ultraviolet.

Looking at resolution only the conclusion is to image in the shortest wavelength possible for monochrome captures where color of the imaged object is not important. Unfortunately another major factor plays an important role in real life imaging:

Seeing

The shorter the wavelength the more light is affected by seeing, the longer the wavelenght the less seeing affects light. Unfortunately this contradicts our wavelength vs. resolution paradigm.
Since the wavelength requirements for best resolution is the opposite of the seeing requirements the imager has to find the best tradeoff between the two by choosing the appropriate wavelength/filter.

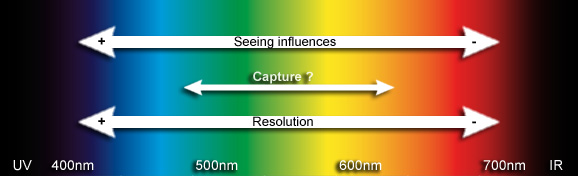
In bad to mediocre seeing conditions the resolution advantage of short wavelengths cannot score - a red bandpass filter or a near IR longpass helps to tame the seeing and make the best out of the conditions but a scope's potential is not utilized. For perfect seeing conditions a blue or even near UV passfilter lets the imager capture the best resolution his scope is capable of. In good but not top seeing a green filter is the best tradeoff between the conflicting requirements.

I saw a number of lunar imagers using an IR-passfilter all the time, no matter what the seeing is like. This is not recommended at all since the airy disk in near IR is very large and limits a scope's resolution significantly! Use an IR-pass only in bad seeing or to record near infrared light explicitly (e.g. albedo features of Mars reflect infrared light from the Sun with high contrast). A quality set of bandpassfilters, preferably with IR blocking included like the Astronomik RGB sets, are highly recommended to be able to adapt to the current conditions and obtain the best images that seeing allows.

The following example images display the difference in resolution and seeing impact between green and near UV. Active solar region 10898 has been captured with a green bandpass filter and an UV longpass with a 6 inch Maksutov Newton scope. The UV capture shows a noticeably higher resolution of details but has suffered much more from seeing: Both recordings have been processed with multiple alignment point processing (MAP) and the regions between the alignment points show blurred areas in the UV recording but not in the green capture - the amplitude of the seeing has been much wider in UV.

Figure 3: Example image in green light and near UV

Of course the free choice of wavelength is only possible for 'colorless' targets like the moon or the sun in integral white light. Colorfull objects like most planets offer limited freedom here.

Finally the spectral sensitivity of the used camera/sensor should be considered. Opt for a wavelength that's recorded with a reasonable sensitivity by the sensor, otherwise long integration times and/or high gain settings might defeat the intended advantages.